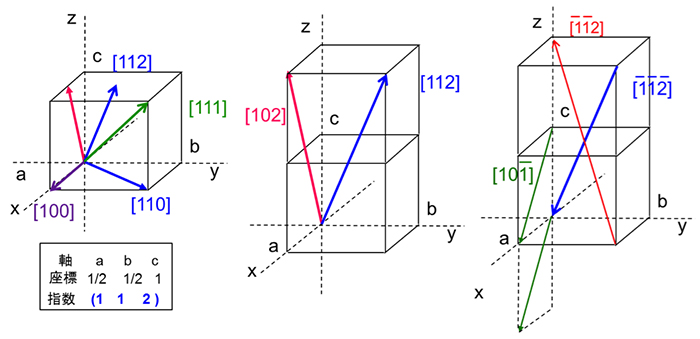
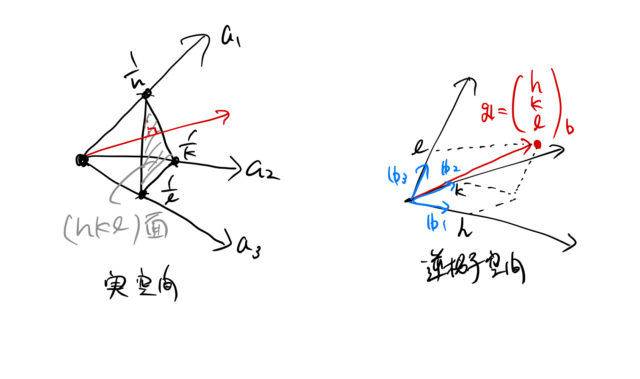
今、 面の格子面間隔を求めることを考えます。 面は、 のそれぞれ に切る平面です。このとき、 面の逆格子ベクトルを とすると、逆格子ベクトルは 面に垂直になります。 そして、 面の格子面間隔 は、 と表されます。 立方晶の場合の格子面間隔13 格子面と面間隔 c a b 3a 2b 2c 図3 ミラー指数 単位格子の外形や格子点の並びで構成される格子面あるい は、結晶の原子で構成される原子面を表す方法にミラー指数と 呼ばれるものがある。面の方程式に倣って切片を利用する方法 である。面の方程式は結晶面の指数 hkl方向とは・・・a 1 a 2 a 3 (hkl)面とは・・・a 1方向に1/h, a 2方向に1/k, a 3方向に1/l, で定義される3点を含む平面 h 1 k 1 l 1 r ha 1 ka 2 la 3 ベクトルrの方向 rに意味はない r hkl方向と(hkl)面は垂直
ミラー指数 面 物理のかぎしっぽ
ミラー指数 面間隔 求め方
ミラー指数 面間隔 求め方-逆格子とミラー指数 8 単位格子のa,b,c軸と(h k l)面を考えると 逆格子ベクトルr* = ha* kb* lc*は(h k l)面と直交し、 (h k l)面の面間隔d (hkl)は1/r*に等しくなる ここで散乱ベクトルkを入射X線ベクトルk 0と 散乱X線ベクトルk 1で表し、その散乱角が2θだとしたら結晶面があるので上述のように(002)面 の一次の反射 と考えてもよいし,(001)面 の2次 の反射と説明するこ ともできる。 一般にX線 結晶学では,(1)式 の反射次数nを1と し て反射の次数を面間隔d,す なわち回折線に対するミラ ー指数の中に含めて表わしている


粉末x線回折測定法の原理と利用法 薬学 これでok
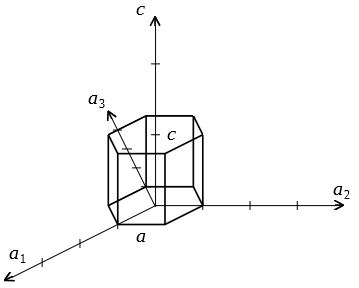
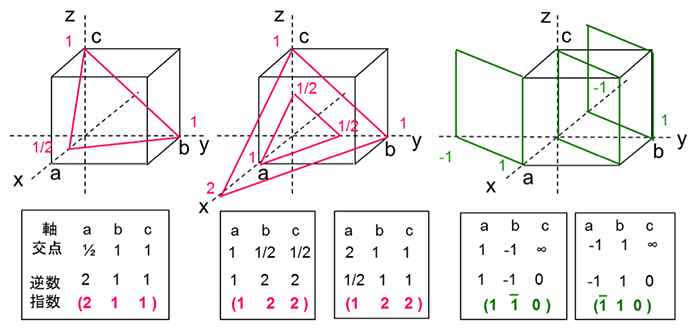
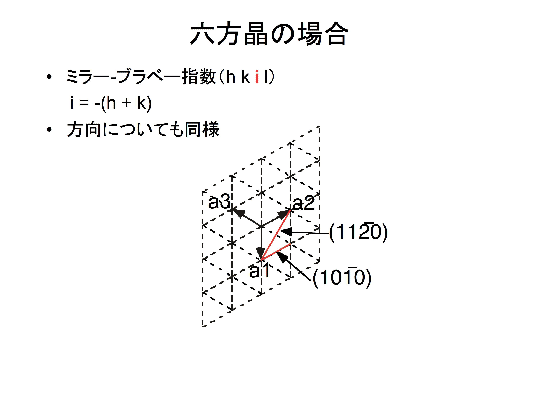
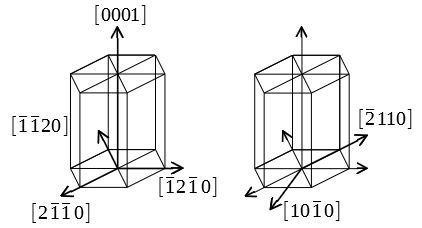
Hkl d hkl = a h2 k2 l2 a:格子定数 面間隔 7\(\{0\}\)面の間隔は\(\{100\}\)面の間隔の半分である。 ミラー指数が\(n\)倍になると、面間隔は\(n\)分の1になる。 六方晶のミラー指数 軸が4本\((a_1,a_2,a_3,c)\)ある点で立方晶と異なるが、基本的なルールは同様である。ミラー指数 (h k j l) をもつ格子面の面間隔を求めよ。 六方晶の格子ベクトルは 逆格子ベクトルは c a x y O A a A ミラー指数 (h k j l) をもつ格子面に対応する逆格子は で 面間隔は 応用
ミラー指数が(hkl)の面間隔dhklと,n倍の(nh,nk,nl)である面間隔dnh,nk,nl の関係 n d d hkl ∴ nhnknl = 図・12 {2}面の間隔は, {110}面の間隔の半分である.一 般に,面{nh,nk,nl}の間隔は, {hkl}面の間隔のn分の1である. ミラー指数(hkl)と{hkl},そしてhklの違いは?という計算で得られる。 反射指数 hkl と面間隔 d, 回折角 2θ のリストを作成する 実験で測定できる回折角 2θ の範囲は有限に限られているから,格子定数から「測定範囲 内に出現しうるすべての反射指数 hklと面間隔値 d,回折ピークの位置 2θ のリスト」を生 成できれば,文献に記載されて2つの面での反射が強め合う条件 d Q G Q1 Q2 Q 1 = Q 2 のとき、面での反射波の位相は 常に揃う 622 逆格子空間での逆格子点の方位ベクトル = ミラー指数 (h, k, l) の格子面 = 回析の条件
ミラー指数:面間隔bを求める公式について 隣接する2つの原子面の面間隔dは、ミラー指数hklと格子定数の関数である。立方晶の対称性をもつ結晶では d=a/√(h^2 k^2 l^2) ・・・(1) となる。Hkl d hkl = a h2 k2 l2 a:格子定数 面間隔 7面配向 P 1 = 00 d 002 = 0344 nm P 1 = 10 d 002 = nm 黒鉛化度と平均面間隔の相関 軸配向 面配向 d 点配向 002 微細組織(配向)毎に 異なる構造歪との相関 P 1 構造歪が減少すれば どの配向でも同じように増加 5


ミラー指数による立方晶 六方晶における面と方向の表し方


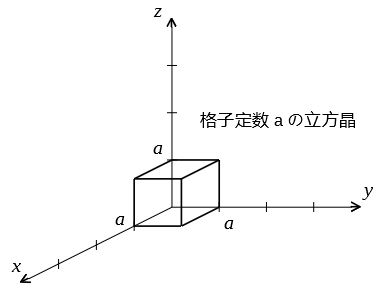
ミラー指数図は格子定数aの立方晶におけるある格子面を 単位格 Yahoo 知恵袋
X線のチャートから物質を同定するには、先ず初めに面間隔を求めます。 自分で面間隔を計算するには、ピークの角度を定規を使って読み取り 次に、この角度をブラッグの式に入れて計算します。 2d・sinθ = nλ (n=1,2,3・・・) ここで求めたい面間隔がd(Å心)や上下面の中心(底心),各面の中心(面 心)のように,元の単位格子の対称性を崩さな いように格子点を加えた格子.全部で14種類 存在する. 体心格子(bodycentered lattice) 底心格子(basecentered lattice) 面心格子(facecentered lattice) 13隣接する2つの原子面の面間隔dは、ミラー指数hklと格子定数の関数である。 立方晶の対称性をもつ結晶では d=a/√(h^2 k^2 l^2)



ミラー指数 面指数 ポップラーン


ミラー指数による立方晶 六方晶における面と方向の表し方
2 (hkl)面と原点との距離(面間隔) ☆面間隔を計算する必要性 ミラー指数(hkl)で表される面どうしの間隔をを計算することは、X線や中性子線回折・ 電子線回折等を用いて結晶構造を解析する際に不可欠なものである。ミラー指数(hkl)で表される面どうしの間隔をを計算することは、X線や中性子線回折・ 電子線回折等を用いて結晶構造を解析する際に不可欠なものである。先にも書いたように、 (hkl)(最大公約数は1)で表される一群の面は、結晶中で等間隔で並んでおり、N = 0の 面は必ず原点を通っている。ミラー指数が(hkl)の面間隔dhklと,n倍の(nh,nk,nl)である面間隔dnh,nk,nl の関係 n d d hkl ∴ nhnknl = 図・12 {2}面の間隔は, {110}面の間隔の半分である.一 般に,面{nh,nk,nl}の間隔は, {hkl}面の間隔のn分の1である.


格子面のミラー指数図は格子定数aの立方晶におけるある格子面を 単位格子内で色を Yahoo 知恵袋


ミラー指数図は格子定数aの立方晶におけるある格子面を 単位格 Yahoo 知恵袋
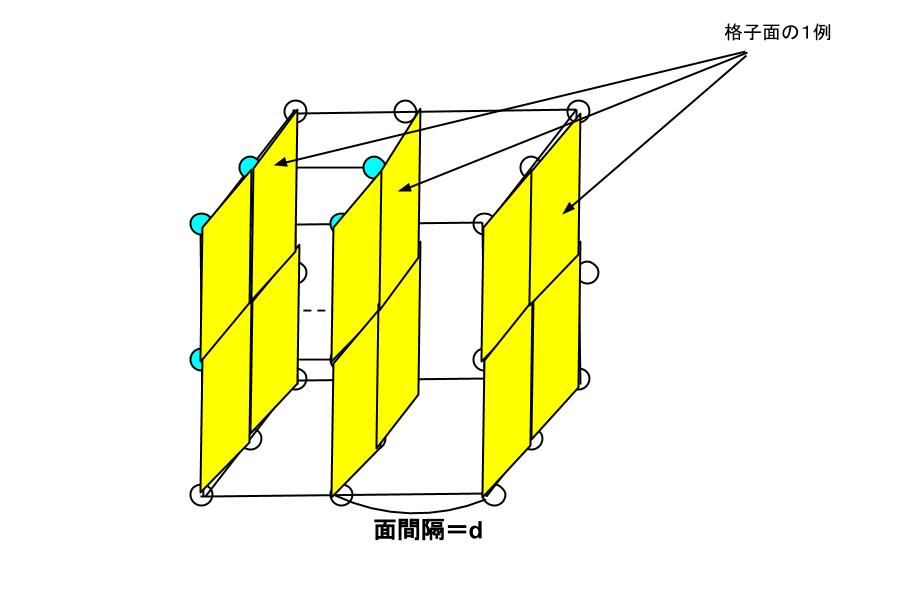
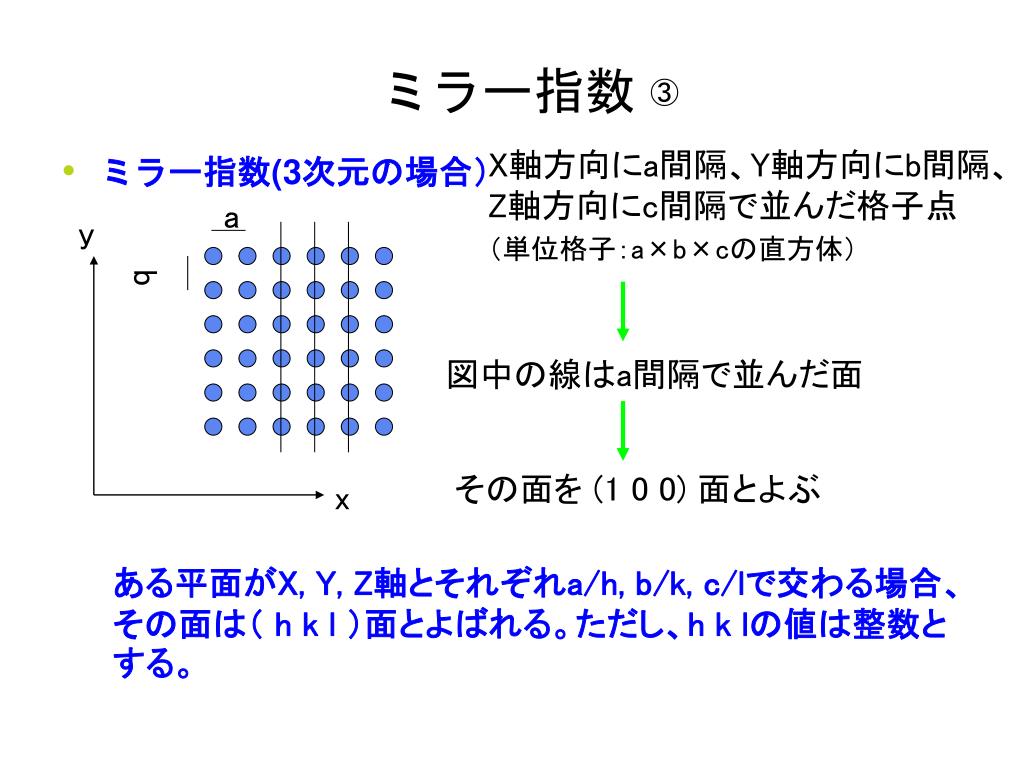
6 ミラー指数その1:結晶における 方向の記述 7 ミラー指数その2:六方晶における ミラー指数 8 面間隔の求め方 9 格子欠陥(原子空孔と転位)・多結晶体 10 x線の発生法・特性x線について 11 ブラッグの条件と面の間隔 12 粉末x線回折による格子定数の求め方となります。これは便宜的に格子面間隔が(d/n)の 結晶面(曲n々 n1)面 による一次の回折に対応します。Bragg条 件の一般形とし ては,回 折線はn次 の回折線であっても,い ずれもそれぞれの (hk1)面 からの一次の回折線と便宜上見なし, 図1単 位胞とミラー指数 14実際の結晶では互いに平行で等間隔の距離で並んでいる結晶面が無数にならんでいるのです. このような1組の面の集合を結晶格子面といいます. 結晶ではこんな結晶格子面がたくさんあります. これを表したいときに使うのがミラー指数(Miller index)です. ミラー指数は というふうに,「丸括弧の中の3つの整数」で表示し,それによって任意の格子面を表現


シリコン格子定数の絶対測定とアボガドロ定数


ミラー指数 面 物理のかぎしっぽ
304 ミラー指数 fdenshicom 更新日:05/02/17 結晶学で等価な原子や原子配列面を参照するために必要な用語のまとめです。ミラー指数の表記 立方晶における主要な面 立方晶における重要な関係 (hkl) !Q ミラー指数:面間隔bを求める公式について 隣接する2つの原子面の面間隔dは、ミラー指数hklと格子定数の関数である。立方晶の対称性をもつ結晶では d=a/√(h^2 k^2 l^2) ・・・(1) となる。



立方晶の面指数 ミラー指数 についてです 先日 テストに出た問題に 物理学 教えて Goo


格子面とミラー指数の求め方
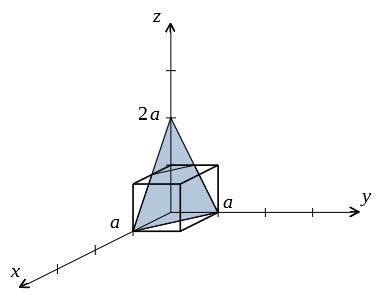
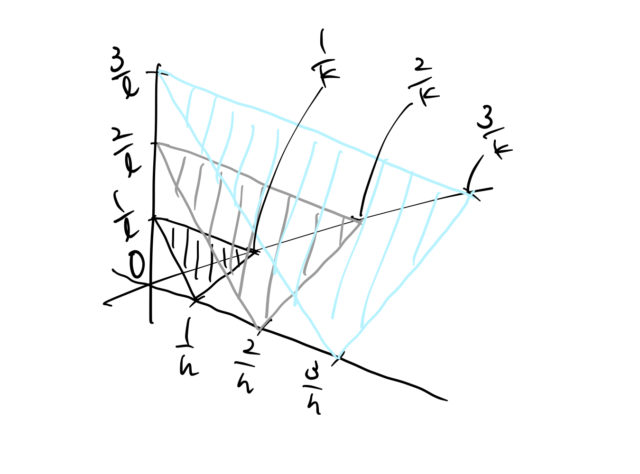
原点に最も近い面 原点に近い面と の交点 a 3 原点に近い面と の交点 b b 2 この面を考える 軸との交点 17 2 33 a 軸との交点 b 17 3 22 OB b b 32, 77 hkcc 整数 7 を掛けて h = 3, k = 2 ミラー指数 (3 2) 413結晶面があるので上述のように(002)面 の一次の反射 と考えてもよいし,(001)面 の2次 の反射と説明するこ ともできる。 一般にX線 結晶学では,(1)式 の反射次数nを1と し て反射の次数を面間隔d,す なわち回折線に対するミラ ー指数の中に含めて表わしているD実空間格子の(hkl)格子面の間隔 λ光の波長 θ格子面と入射光のなす角 上の式の(hkl)は、格子面のミラー指数である。 ブラッグの反射条件は、結晶によるX線回折を考えるときに使われる。


ダイヤモンドの結晶と欠陥 中央宝石研究所 Cgl


x線結晶解析におけるラウエの条件式とブラッグの条件式
Q ミラー指数:面間隔dを求める式について 隣接する2つの原子面の面間隔dは、ミラー指数hklと格子定数の関数である。立方晶の対称性をもつ結晶では d=a/√(h^2 k^2 l^2) となる。 なぜこうなるのか証明せよといわれたのですが どうやってすればよい332六方格子のミラー指数 図312六方格子のミラー指数 立方格子との相違→a1,a2,a3,c の4軸を考える点 a1,a2,c 軸をα,β,δで横切る面 a/α :a/β :c/δの最小の整数比h:k:m を求める. 次に最後の指標をl=(hk) のように決める.次に、ミラー指数(Miller indices) hklは格子面によって定 義される。ただし、ここでh, k, lは正数の組み合わせである。単位格子のa, b, c軸をそれ ぞれa/h, b/k, c/lの長さで切る面を(hkl)面とする。


ダイヤモンドの結晶と欠陥 中央宝石研究所 Cgl


図2 1図2 2図2 3の結晶面のミラー指数を教えてください よ Yahoo 知恵袋
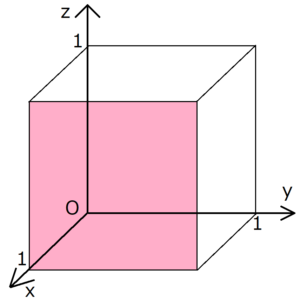
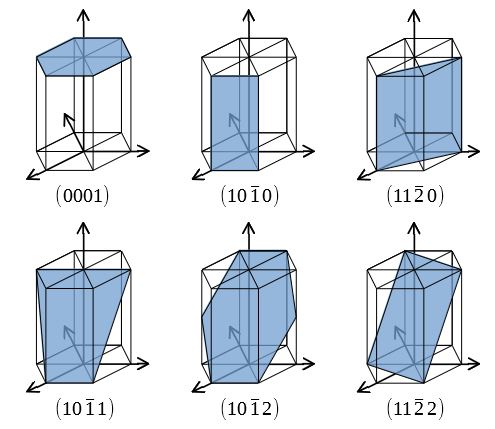
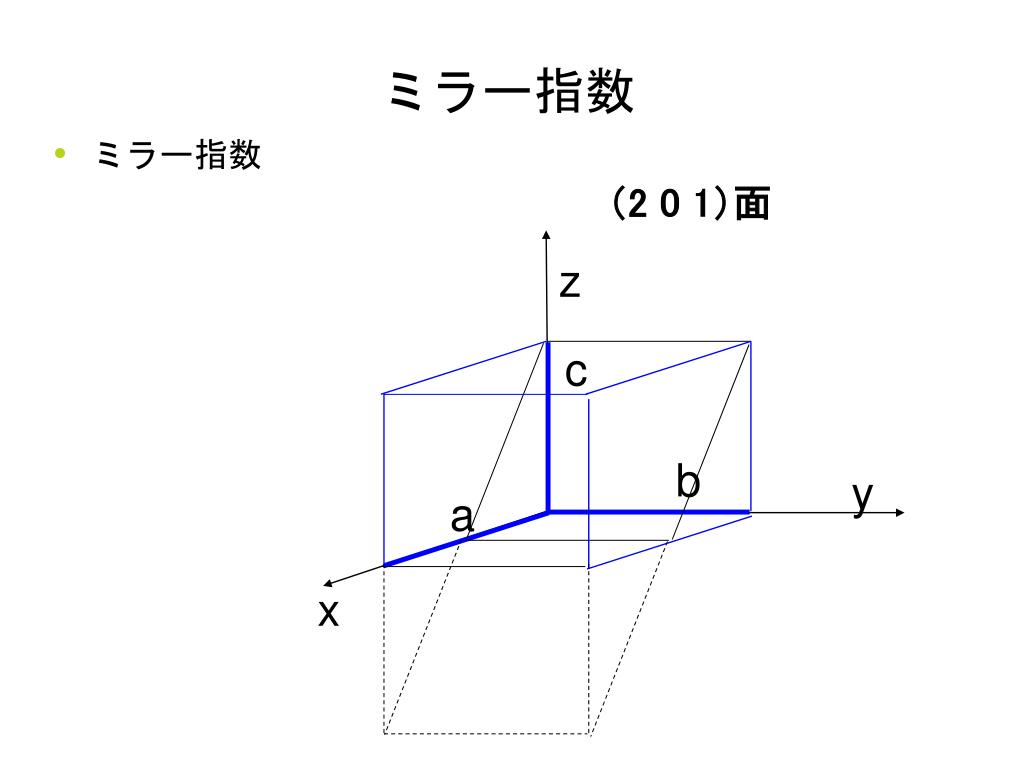
Q ミラー指数:面間隔bを求める公式について 隣接する2つの原子面の面間隔dは、ミラー指数hklと格子定数の関数である。立方晶の対称性をもつ結晶では d=a/√(h^2 k^2 l^2) ・・・(1) となる。) 面は直接格子の基本並進ベクトル a, a, a を 1 2 3 1/ h, 1/ k, 1/ l で切る平面のことである(ミラー指数のこと)。 (hkl)面とそれに垂直な逆格 子ベクトル K hkl 前ページの図に示すように、 逆格子ベクトル K hkl は(h k l) 面に垂直 であること意味しているミラー指数(面) 5 仮に,上の単位格子が立方晶だとすると(100),(010),(001) は等価な面です.立方体はa,b,c どの軸で も90 度回せばもとにもどりますから,(100) の図をc 軸の回りに90 度回せば(010) の図になります. (010) の図をa 軸の回りに90 度回せば(001) の図になります.図にはありませんが(100) と



ミラー指数 面指数 ポップラーン
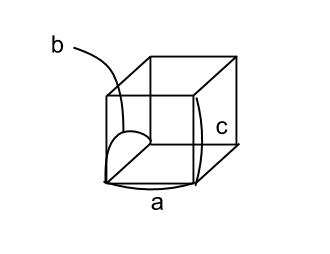


粉末x線回折測定法の原理と利用法 薬学 これでok
ミラー指数 (h k j l) をもつ格子面の面間隔を求めよ。 六方晶の格子ベクトルは 逆格子ベクトルは c a x y O A a A ミラー指数 (h k j l) をもつ格子面に対応する逆格子は で 面間隔は 応用ミラー指数の表記 立方晶における主要な面 立方晶における重要な関係 (hkl) !ミラー指数 • 結晶面の指数 原子の間隔・・・数Å ようなもの 原子の間隔(格子定数)以下のプローブを使う必要がある Braggの式 a 原子面の間隔によって生じる入射波と反射波の行路差


シリコン格子定数の絶対測定とアボガドロ定数



粉末x線回折測定法の原理と利用法 薬学 これでok



結晶格子の格子定数 大きさを定める定数 化学徒の備忘録


ミラー指数 面 物理のかぎしっぽ


放課後化学講義室 X線回折のデータ解析をするプログラム


結晶面の面間隔


ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら
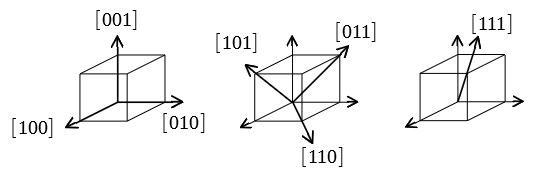


ミラー指数による立方晶 六方晶における面と方向の表し方


結晶の面と方向の記述方法



ミラー指数で表された面の図の書き方 化学徒の備忘録



ミラー指数による立方晶 六方晶における面と方向の表し方


岩塩のミラー指数 100 110 111 の格子面間隔d100 D Yahoo 知恵袋


ミラー指数 面 物理のかぎしっぽ


ミラー指数による立方晶 六方晶における面と方向の表し方


岩塩のミラー指数 100 110 111 の格子面間隔d100 D Yahoo 知恵袋


化学の問題です 教えてください この2つの図を使って格子面間隔と 格子定 Yahoo 知恵袋


ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら


格子面とミラー指数の求め方


Information


ミラー指数による立方晶 六方晶における面と方向の表し方


ミラー指数 面 物理のかぎしっぽ


ミラー指数による立方晶 六方晶における面と方向の表し方



Xrdの原理と解析方法 わかること x線回折装置とは
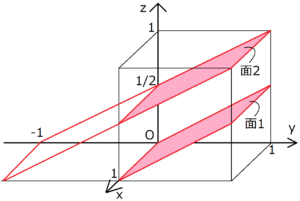


格子面とミラー指数の求め方
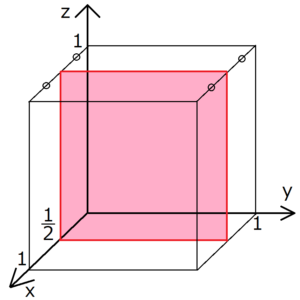


格子面とミラー指数の求め方
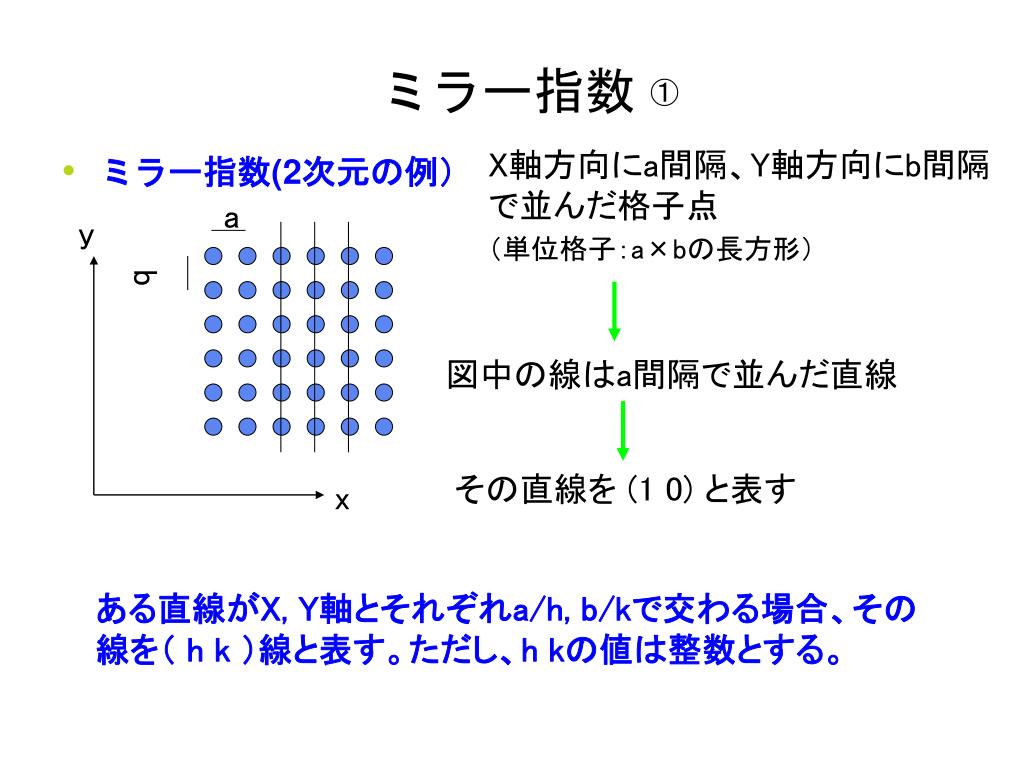


Ppt ミラー指数 2 次元の例 Powerpoint Presentation Free Download Id
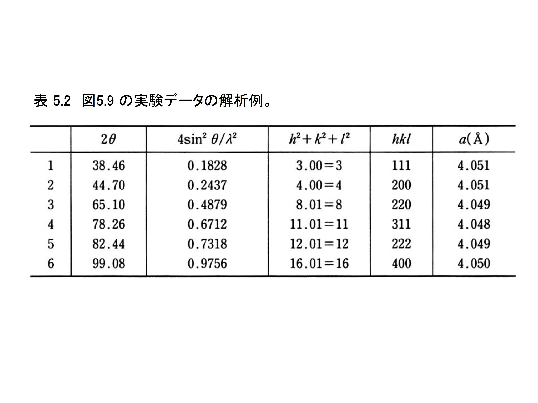


粉末x線回折による解析例



ミラー指数で表された面の図の書き方 化学徒の備忘録



金属材料の基礎知識 ものづくり まちづくり Btob情報サイト Tech Note
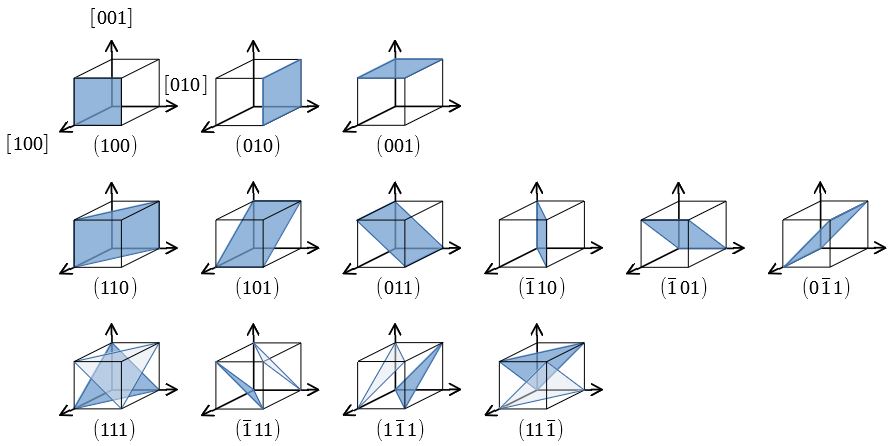


ミラー指数による立方晶 六方晶における面と方向の表し方
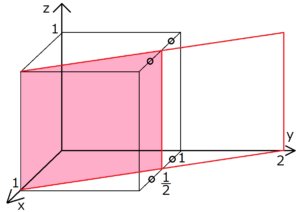


格子面とミラー指数の求め方


ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら


データの解析 鉱物種の同定 戻る まず x線粉末回折で得られた下の回折チャート 特性x線 cuka 1 5418aで測定 を例として説明する 最初は x線回折データは回折チャートのピークの頂点 黒の三角矢印で示したのがピークの頂点 が


Ppt ミラー指数 2 次元の例 Powerpoint Presentation Free Download Id


ミラー指数について 100 面の面間隔と 0 面の面間隔 Yahoo 知恵袋



ミラー指数で表された面の図の書き方 化学徒の備忘録



ミラー指数で表された面の図の書き方 化学徒の備忘録


5 5


Ppt ミラー指数 2 次元の例 Powerpoint Presentation Free Download Id



04 号 x線回折による応力測定法 Astamuse


ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら
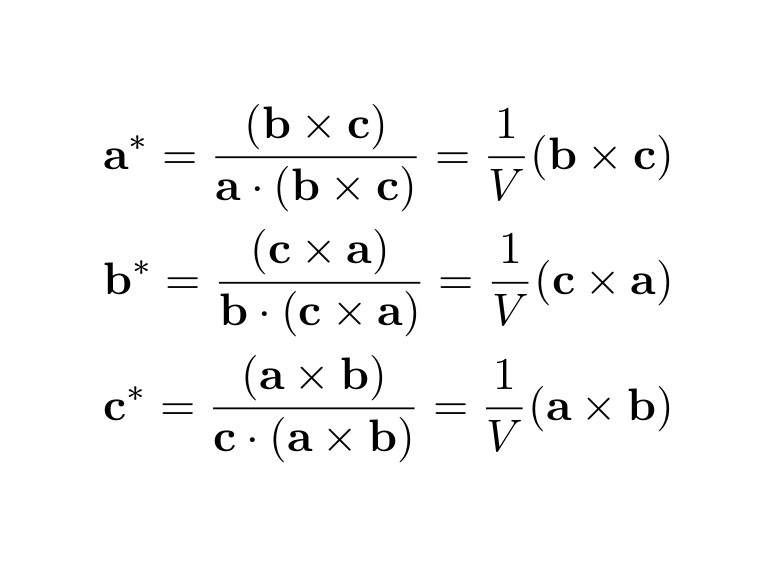


逆格子点の計算の理論背景 Theoretical Background For Calculation Of Reciprocal Lattice And Reciprocal Lattice Points To Cause Diffraction
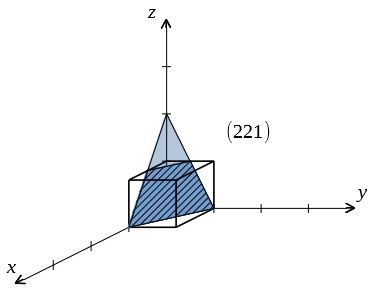


ミラー指数による立方晶 六方晶における面と方向の表し方


ミラー指数が 101 のとき格子面が図のようになりました この Yahoo 知恵袋



前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download



金属材料の基礎知識 ものづくり まちづくり Btob情報サイト Tech Note


ミラー指数 面 物理のかぎしっぽ



電子線照射用試料 B Lial の 育成とその電気的特性の測定 矢萩 橋本研究室 工 E 阿部 信介 Ppt Download


放課後化学講義室 X線回折のデータ解析をするプログラム



ブラベー格子 三方晶 大学で三方晶 菱面体 の角度の関係をa B 90 G 物理学 教えて Goo


x線結晶解析におけるラウエの条件式とブラッグの条件式
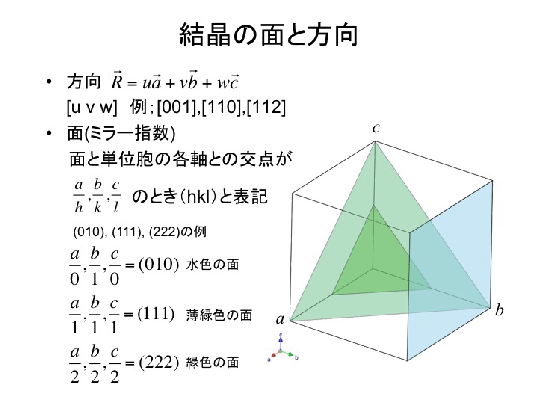


結晶の面と方向の記述方法



0 件のコメント:
コメントを投稿