6/3/21 · メネラウスの定理の覚え方1 ・メネラウスの定理は「六点からなる(キツネのような形の)図形に対して成立する定理」と認識する立場です。 あとは,順々に比をとっていきます。 比の順番の覚え方は自由です。 ちなみに僕はキツネの頭からはじめて · チェバの定理とメネラウスの定理をてんびん算と連比で解く チェバ・メラをてんびん算で攻略2/10/19 · チェバ・メネラウスの定理が使えるようになると何が出来るのか メネラウスの定理が使えると、ベクトルの問題で重宝します。 特にセンタータイプの答えだけ入れていくような問題の場合は、大幅に時間を短縮できます。 直接、答えを求める問題でなく

高校 数学a 図形20 メネラウス定理2 10分 Youtube
チェバの定理 メネラウスの定理 問題
チェバの定理 メネラウスの定理 問題-Mathaquarium定理・公式の証明メネラウスの定理,チェバの定理 1 1 メネラウスの定理 abc の3 辺bc,ca,ab 上,またはそれらの 延長上にそれぞれ三角形の頂点と異なる点p,q,r がある。3 点p,q,r が一直線上にあるならば,次 の等式が成り立つ。 1 rb ar qa cq22/4/19 · 0701チェバの定理、メネラウスの定理(難易度1) 19/4/22 問題 三角形 A B C において、 A B 上に点 、 D 、 B C 上に点 、 E 、 A C 上に点 F をとるとき以下の問いに答えよ。 (1) 、 、 、 、 A D = 5 、 D B = 4 、 A F = 6 、 F C = 2 、 B C = 10 のとき、 B E の長さを求めよ (2) 、 、 、 A D = 5 、 D B = 4 、 D G = 3 、 G C = 2 のとき、 B E E C の比を求めよ ヒント




平面図形18 メネラウスの定理の逆 怜悧玲瓏 高校数学を天空から俯瞰する
よって, A B C \triangle\mathrm {ABC} ABC の頂点から傍接円に引いた接線の長さはいずれも A B C \triangle\mathrm {ABC} ABC の周の長さの半分である (2) (1) の結果により, B P = B T = A T − A B = s − c \mathrm {BP} = \mathrm {BT} = \mathrm {AT}\mathrm {AB} = sc BP = BT = AT− AB = s−c が成15/8/19 · チェバの定理 三角形abcの頂点 a, b, c と, この三角形の辺及びその延長上に無い点oを結ぶ 各直線が対辺またはその延長とそれぞれ点p, q, rで交わるとき, 次の等式が成り立つこの問題は、まずbp:pcの線分比を チェバの定理 で求めるのがポイントだよ。 POINT 「面積比」は「底辺と高さ」に注目
15/1/19 · 今回は数aの範囲から、チェバ・メネラウスの定理と三角形の面積比の問題を扱います。 チェバ・メネラウスの定理から確認していきましょう。 次に線分の比と三角形の面積比の関係を見てみよう。 「高さが同じ長さの場合、底辺の比が面積比」 右図のようなとき、 abpと acpは高さが同ブックマークを追加 高校数学Aチェバの定理とメネラウスの定理の基本問題演習 受験の月 1 user examistjp 禁止事項と各種制限措置について をご確認の上、良識あるコメントにご協力ください 0 / 100 入力したタグを追加 twitterにシェア あとで読む 非16/9/18 · こんにちは。 da Vinch (@mathsouko_vinch)です。 チェバの定理・メネラウスの定理とはまず。チェバの定理とメネラウスの定理は「比に関する定理」です。さらに「三角形に対して使っていく定理」なのでそれを忘れないようにし
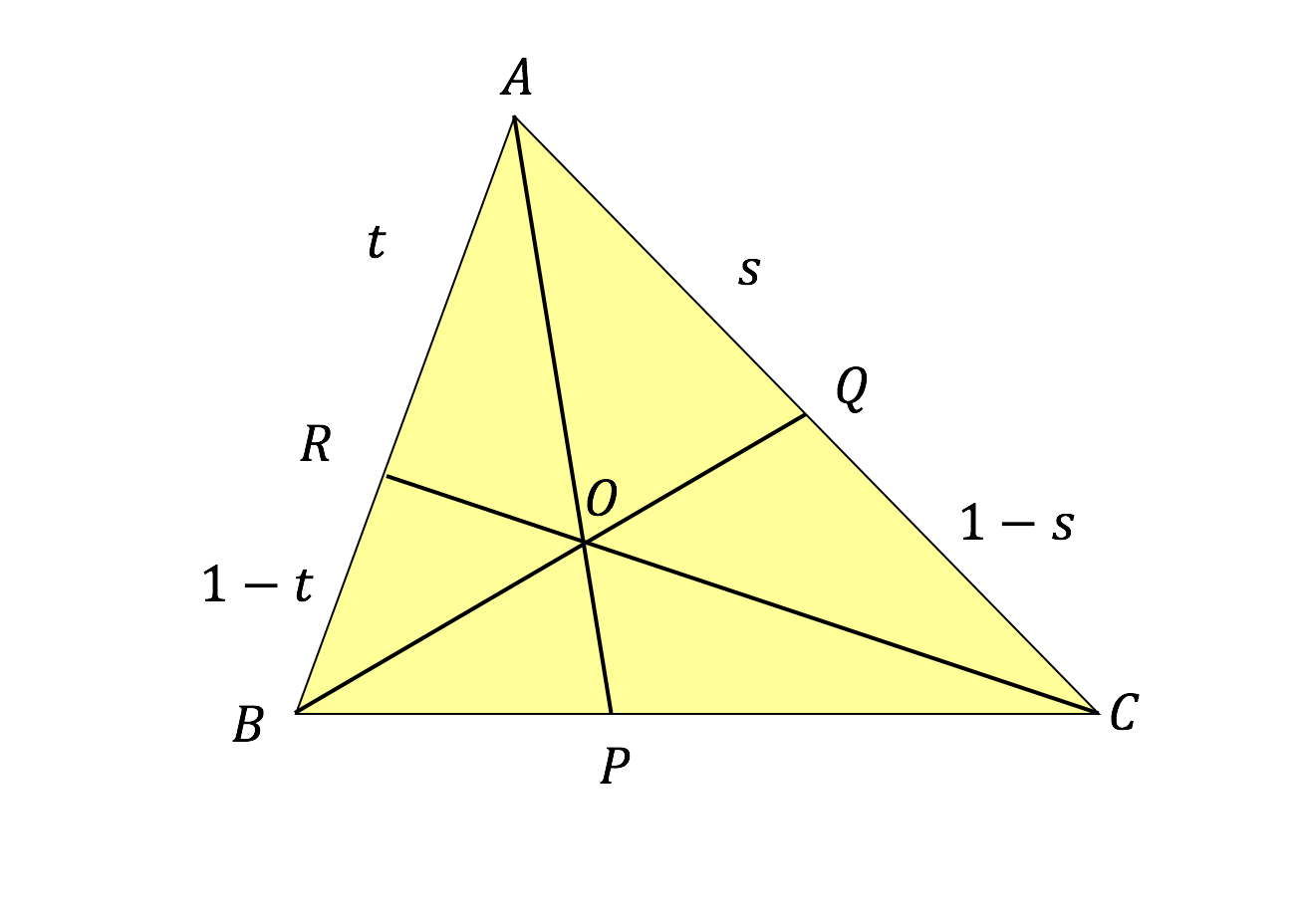
3 チェバの定理の逆,メネラウスの定理の逆 (チェバの定理の逆) ABCの3辺AB,BC,CA上に点P,Q,Rがある。このとき, 1 RA CR QC BQ PB AP ならば,AQ,BR,CPは1点で交わる。 (メネラウスの定理 · チェバの定理とメネラウスの定理の基本問題演習 三角形の五心① 三角形の重心とその存在証明 三角形の五心② 三角形の内心とその存在証明かんたんメネラウスの定理・チェバの定理 それでは「メネラウスの定理」や「チェバの定理」を知らなくても、上記の三角形の質点と重心を利用して解けることをご説明します。 下の図の問題は (1)が「メネラウスの定理」を用いて解く問題 (2)が「チェバの定理」を利用して解く問題



3分で分かる チェバの定理をわかりやすく 証明も徹底解説 合格サプリ



メネラウスの定理とは 証明や覚え方 問題の解き方 受験辞典
4/4/ · チェバの定理、メネラウスの定理 中学受験の問題を作成される中学の先生は先に種々の定理が頭にあって、その定理を知らないであろう小学生に定理を使わせずに解かせようとすると問題を散見します。 チェバの定理、メネラウスの定理の問題も何回も28/8/10 · メネラウスの定理と、チェバの定理を使った問題について、質問があります。 久しぶりにこの定理の復習をしようと思って問題に取り組んでみたのですが・・・どうにも答えが出ませんでして(;_;) 問題は2つ(3つ)あり17/6/17 · 中2 チェバの定理とメネラウスの定理 中学生 数学のノート Clear 表紙 1 2 3 公開日時 17年06月17日 11時32分 更新日時 年08月23日 01時33分 中学生 2年生



チェバの定理やメネラウスの定理は不要 辺比と面積比の関係だけでカンタンに解く方法を伝授 Youtube




高校数学a チェバの定理とメネラウスの定理の基本問題演習 受験の月
7/11/19 · 中学受験算数で学習するテクニックの1つとして、 「天秤法(天秤算)」 というものがあります。 こちらを利用することで、学生が一度は苦しむであろう難問を解くことができるようになるのです。 大学受験であれば 「チェバの定理」 や 「メネラウスの定理」 を用いる問題です。 高校受験であれば 「食塩濃度」 に関する問題です。 「公式が長くて要は,メネラウスの定理やチェバの定理と関係していて,下の図の \(\mbox{AE}\mbox{EB}\) や \(\mbox{OP}\mbox{PE}\) などの比の値が簡単に求められるって話しなんだ。 これって,二つの定理で解けるでしょ。やってみよう。まずはチェバの定理だね/5/17 · メネラウスの定理 と チェバの定理 は、三角形の3辺について、 内分比や外分比によって得られる比の値の積が1になる定理 です。




チェバの定理の逆 メネラウスの定理の逆 超わかる 高校数学 A 授業 図形の性質 23 Youtube




数学a 図形の性質 チェバの定理 メネラウスのの定理 問題 Youtube
28/3/ · 練習問題①「チェバ、メネラウスの使い分け」 練習問題②「チェバの定理の逆で証明」 チェバの定理とは、 三角形と、その各頂点から向かい合う辺へ引いた線分の間に成り立つ定理 です。17/2/ · 高校数学の要点, 無料の練習問題, 例題と解説 チェバの定理・メネラウスの定理チェバの定理とメネラウスの定理 金沢光則 平成21 年2 月9 日 1 はじめに 昔、平面図形が高校の教材でなかった頃、ベクトルの問題で線分の比を求めるものを、チェバやメネラウ スを使えば簡単に解けるという話題で盛り上がっていたことがあった。




数学a 平面図形 メネラウス チェバの定理 まとめ集 自宅でできる受験対策ショップ ワカルー Wakaru



3分で分かる チェバの定理をわかりやすく 証明も徹底解説 合格サプリ
12/8/19 · チェバの定理は、三角形と3つの頂点を通る直線に関するわりと有名な定理です。 関連する辺の比の積が1となる、美しい形をしています。 証明は、いくつかあります。 本稿では、メネラウスの定理を2回使います。 まず、 abpと直線crに着目します。15/1/19 · メネラウスの定理 ABCの辺BC, CA, ABまたはその延長が1つの直線とそれぞれ点P, Q, Rで交わるとき が成り立つ。 ※チェバの定理・メネラウスの定理ともに、3組の線分の長さの比の積が1となるという式である。 つまり実際の長さがわかっていなくても比がチェバの定理の証明 図のように、a= BCG、b= CAG、c= ABGとします。 AF/BF=b/a、BD/CD=c/b、CE/AE=a/c より、 (AF/BF)(BD/CD)(CE/AE)=(b/a)(c/b)(a/c)=1 メネラウスの定理の証明 図のように、a= BCG、b= CAG、c= DCGとします。 AF/BF=b/a、BC/CD=a/c、DG/AG=c/b より、




メネラウス の 定理 メネラウスの定理




メネラウスの定理 Menelaus S Theorem Japaneseclass Jp
3/11/ · 問題解説図形①~チェバ・メネラウスの定理~ 投稿者 ssw_okaka 投稿公開日 年11月3日 投稿カテゴリー 図形 / 高校数学 投稿コメント 0件のコメントメネラウス・チェバの定理のちょっとした小手技 札幌旭丘高校 中村文則 メチェっていざ周遊の旅へでかけよう! メネラウスの定理は三角形の辺を直線で切るときの分点に成立する性質だけ方べきの定理 方べきの定理はなぜ成り立つのか。 いずれのケースも、三角形の相似から説明されます。 1.点 \(p\) が円の内部にあるとき 円周角の定理から、下図の赤い角、ピンクの角がそれぞれ等しいため、 クリーム色の三



チェバの定理




高校数学復習記録 その8 桜花 現役バイト塾講師 Note
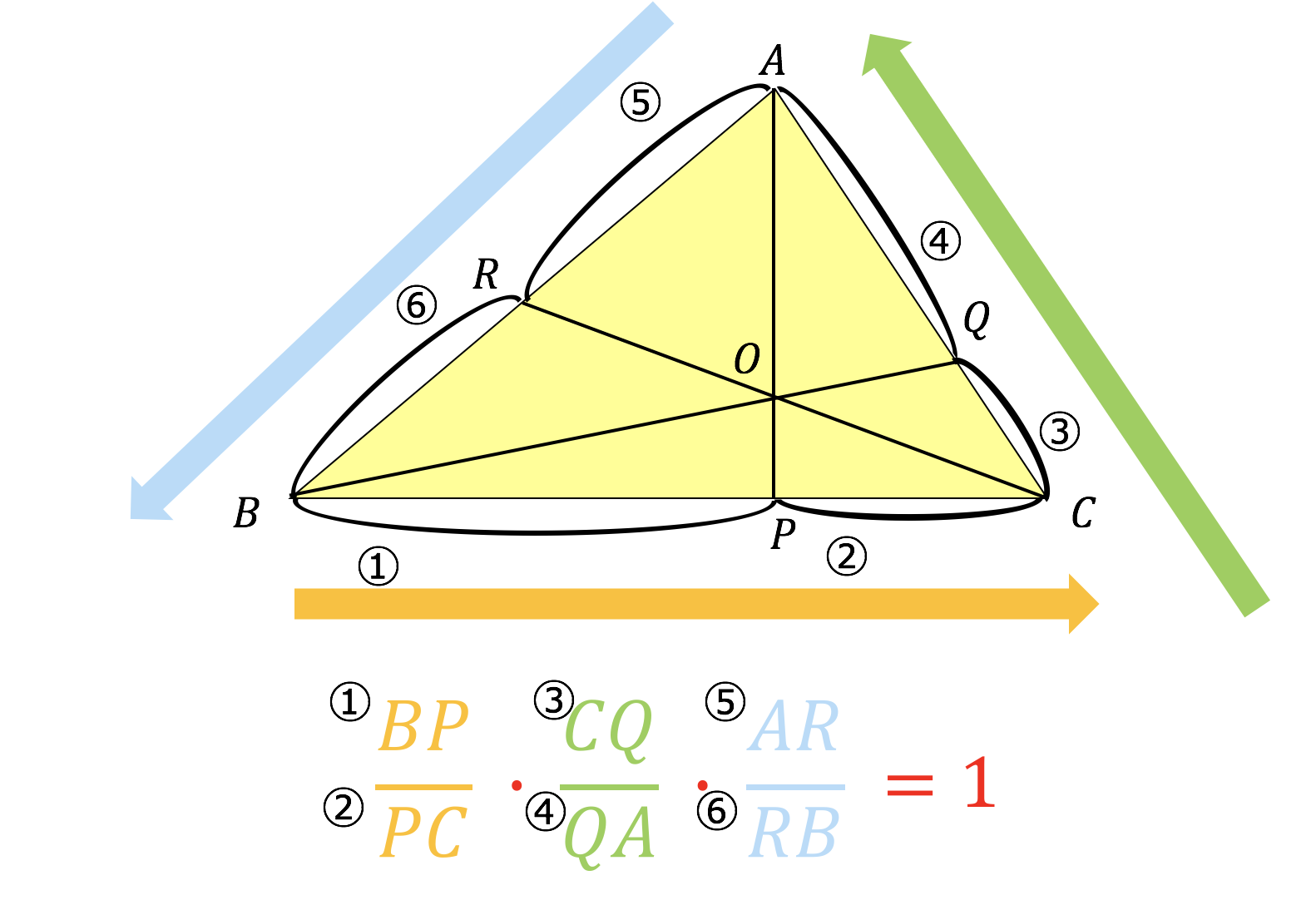
メネラウスの定理 チェバの定理 ・性質を形式的に暗記するだけでなく,いろいろな証明法やその考え方を問題解決に結び付けるように指導する。 知識・理解 角の二等分線の性質や与えられた定理を正しく理解できる。 展 開メネラウスの定理では3点 P, Q, R は1直線上に並びますが,チェバの定理では,それぞれ辺 AB, BC, CA にあります. (公式の見方) 右図のように,頂点 A からスタートして,交点 P までの長さを分子(上)とし,次に,交点 P から頂点 B までの長さを分母(下)とする.以下同様に分数を掛けて行って,頂点 A まで戻ったら,それらの分数の積が1になるという意味 機械(2) 四角形におけるメネラウスの定理 四角形におけるメネラウスの定理について考察する。 この場合にも,チェバの定理の場合と同様に2 つの三 角形を辺で貼り合わせて四角形を構成するという方法 を用いる。メネラウスの定理には三角形のある一辺で




改訂版 クリアー数学a P132 12 チェバの定理 メネラウスの定理
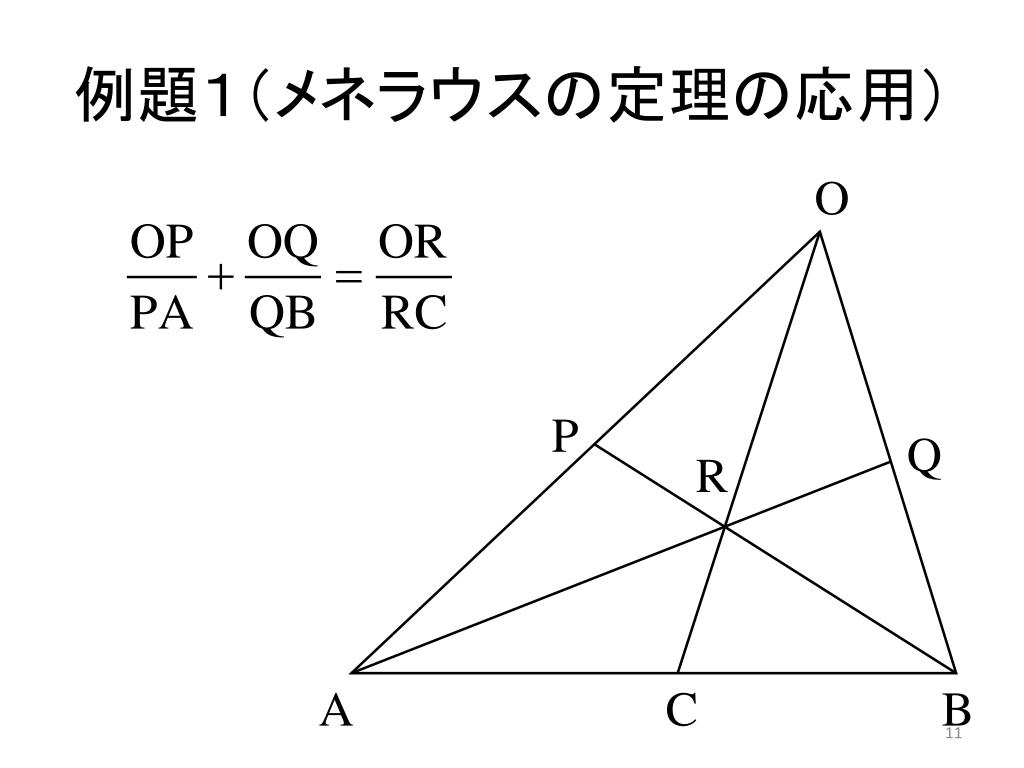



Ppt 数学のかた ち Powerpoint Presentation Free Download Id
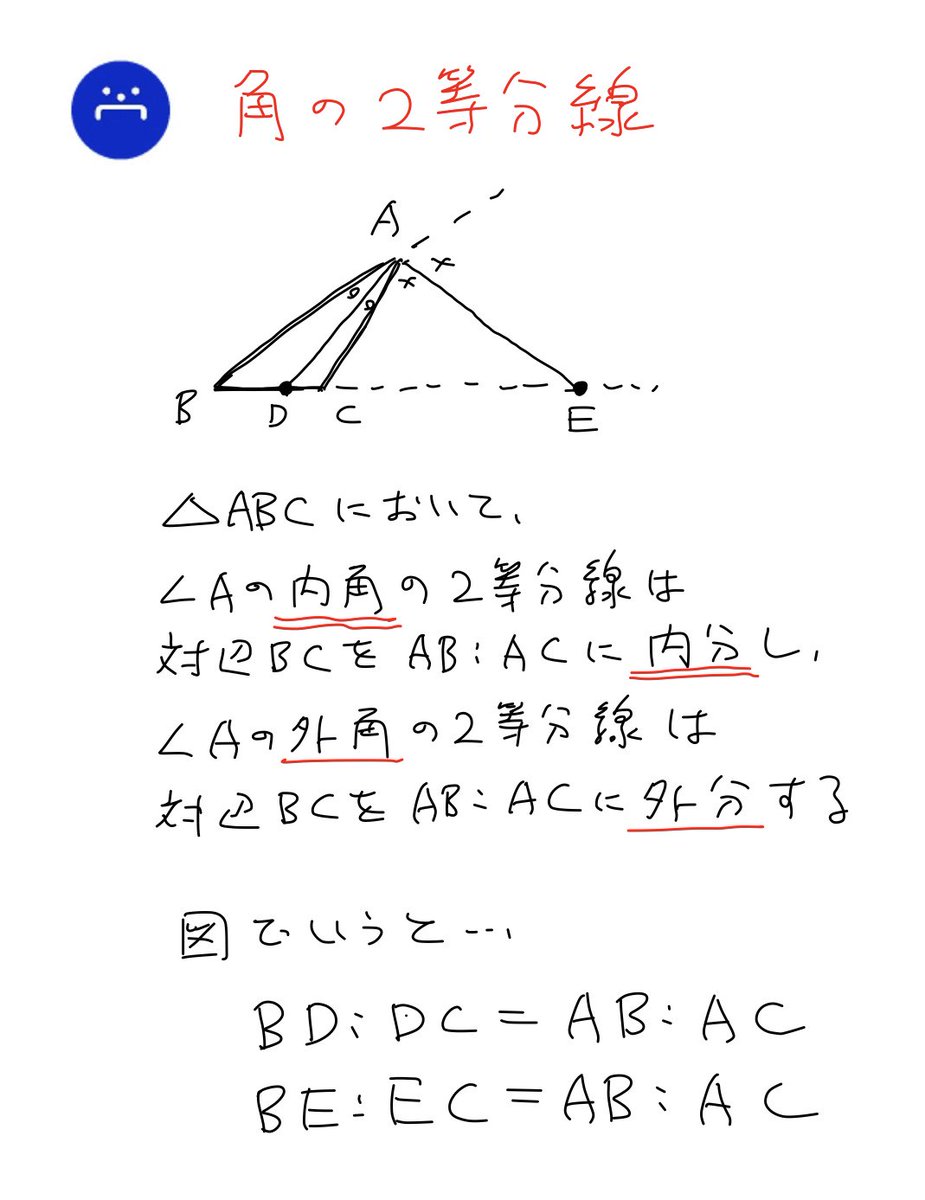
チェバの定理とメネラウスの定理の本質 チェバの定理とメネラウスの定理の本質 Watch later Share Copy link Info Shopping Tap to unmute If playback#2 メネラウスの定理とチェバの定理 ¶ 正しくない「チェバの定理の逆」 ‡ 3 点d,e,f をそれぞれ4abc の3 辺bc,ca,ab の内分点または外分点とする。 それらのうちの奇数個が内分点,偶数個が外分点で,かつ,等式 af fb × bd dc × ce ea = 1 が成り立つならば,3 直線ad,be,cf は共点である。練習問題 46 チェバの定理・メネラウスの定理 check1 2 check3 a c r s q b p 右図に示すように, ab =√3, bc =2, ca =1 で, ∠a =90°の直角三角形 abc がある。頂点a から辺bc に下した垂線の足を p, 辺ac の中点 をq とおき, 線分ap と線分bq の交点 をr とおく。また, 直線cr と辺ab の



メネラウスの定理 チェバの定理 京極一樹の数学塾




メネラウスの定理




チェバの定理まとめ 証明 覚え方 逆 問題 理系ラボ




改訂版 クリアー数学a P133 補 チェバの定理の逆 メネラウスの定理の逆
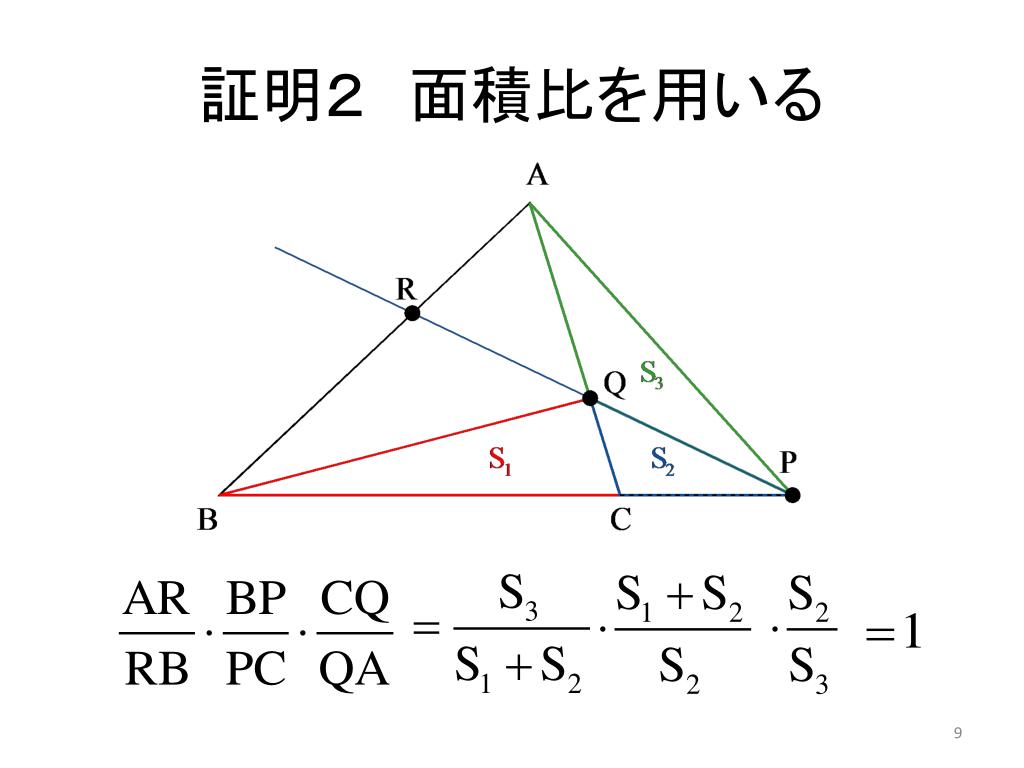



Ppt 数学のかた ち Powerpoint Presentation Free Download Id




メネラウス チェバの定理を追加しました 中学数学 高校数学のサイト ときどき大学数学




改訂版 クリアー数学a P133 補 チェバの定理の逆 メネラウスの定理の逆




Ppt 数学のかた ち Powerpoint Presentation Free Download Id




高校数学a チェバの定理1 基本 練習編 映像授業のtry It トライイット



チェバの定理とは 証明や覚え方 メネラウスの定理との違い 受験辞典




高校数学a メネラウスの定理2 応用 例題編 映像授業のtry It トライイット




高校数学a メネラウスの定理2 応用 例題編 映像授業のtry It トライイット




慶應生紹介 メネラウスの定理の覚え方はコレだ 証明 問題付き 高校生向け受験応援メディア 受験のミカタ




平面図形11 メネラウスの定理の逆 怜悧玲瓏 高校数学を天空から俯瞰する



Tossランド チェバの定理 メネラウスの定理



メネラウスの定理とは 証明や覚え方 問題の解き方 受験辞典




チェバの定理




チェバの定理は 三角形の内部にある点xと3頂点を結んだ直線が 3辺と交わる時に成り立 Clear




高校数学a チェバの定理2 応用 練習編 映像授業のtry It トライイット



チェバの定理とは 証明や覚え方 メネラウスの定理との違い 受験辞典




チェバの定理の証明 覚え方を早稲田生が紹介 問題付き 高校生向け受験応援メディア 受験のミカタ




チェバの定理の証明 覚え方を早稲田生が紹介 問題付き 高校生向け受験応援メディア 受験のミカタ




チェバの定理は 三角形の内部にある点xと3頂点を結んだ直線が 3辺と交わる時に成り立 Clear
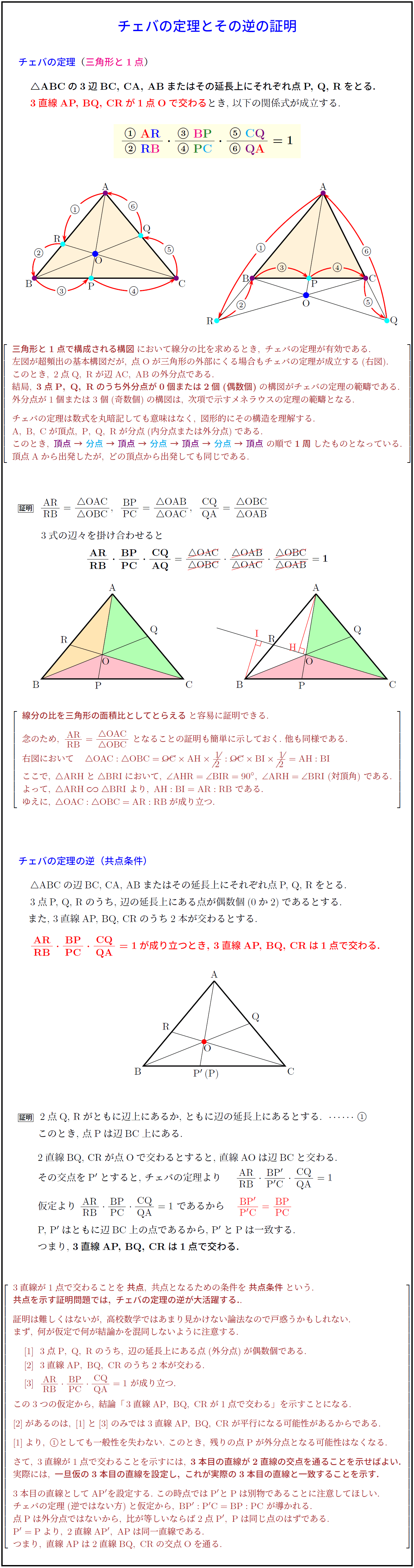



高校数学a チェバの定理とその逆の証明 受験の月



メネラウスの定理とは 証明や覚え方 問題の解き方 受験辞典




チェバの定理の証明 覚え方を早稲田生が紹介 問題付き 高校生向け受験応援メディア 受験のミカタ




平面図形18 メネラウスの定理の逆 怜悧玲瓏 高校数学を天空から俯瞰する




解説をお願いします 答えは9 でした Clear




中3数学 相似 No 12 チェバの定理 メネラウスの定理 Youtube



チェバの定理とは 証明や覚え方 メネラウスの定理との違い 受験辞典




チェバの定理とメラネウスの定理を理解し問題を解ける Himokuri




平面図形9 メネラウスの定理 怜悧玲瓏 高校数学を天空から俯瞰する
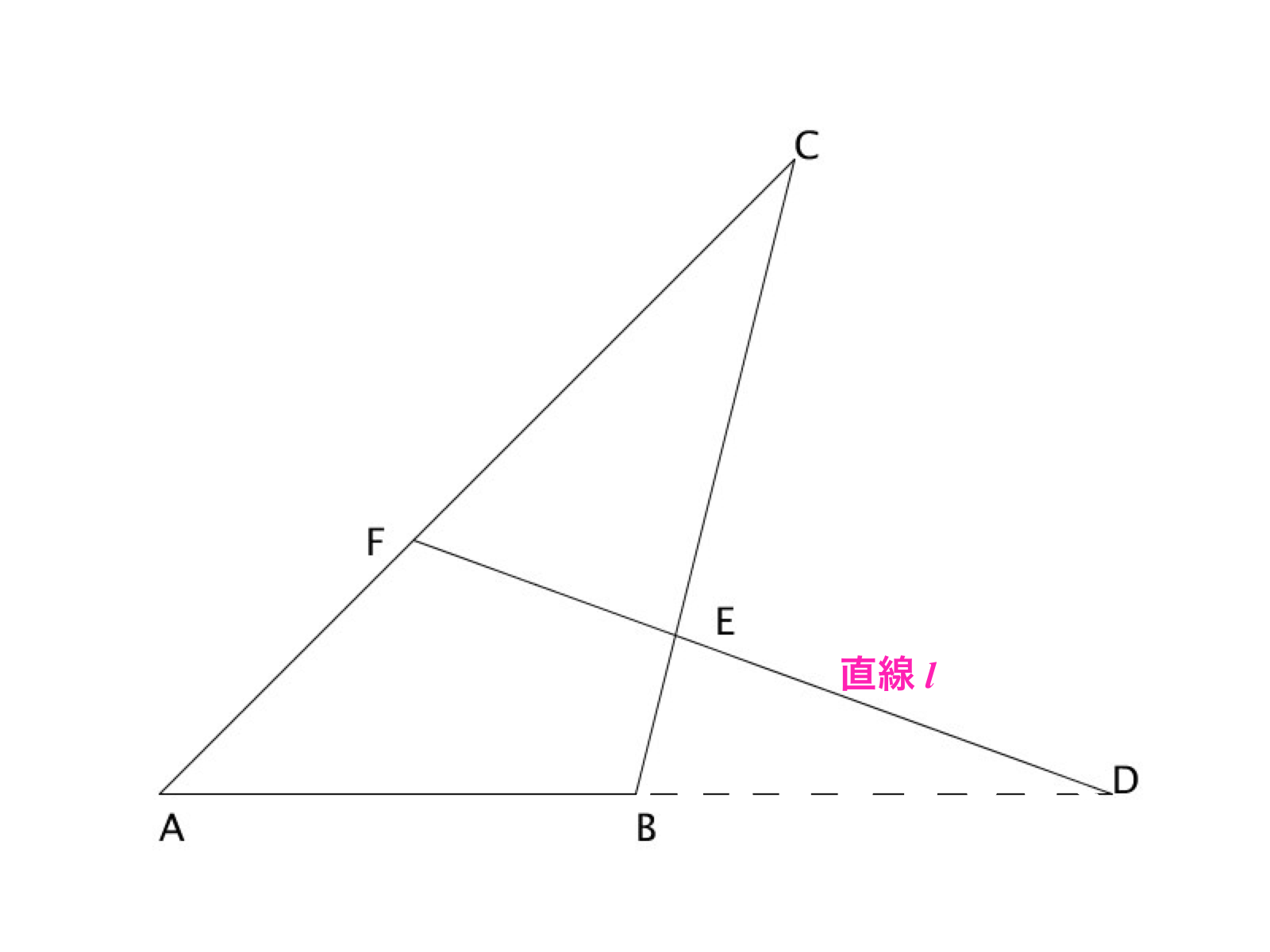



3分で分かる メネラウスの定理とその証明 使い方など 合格サプリ
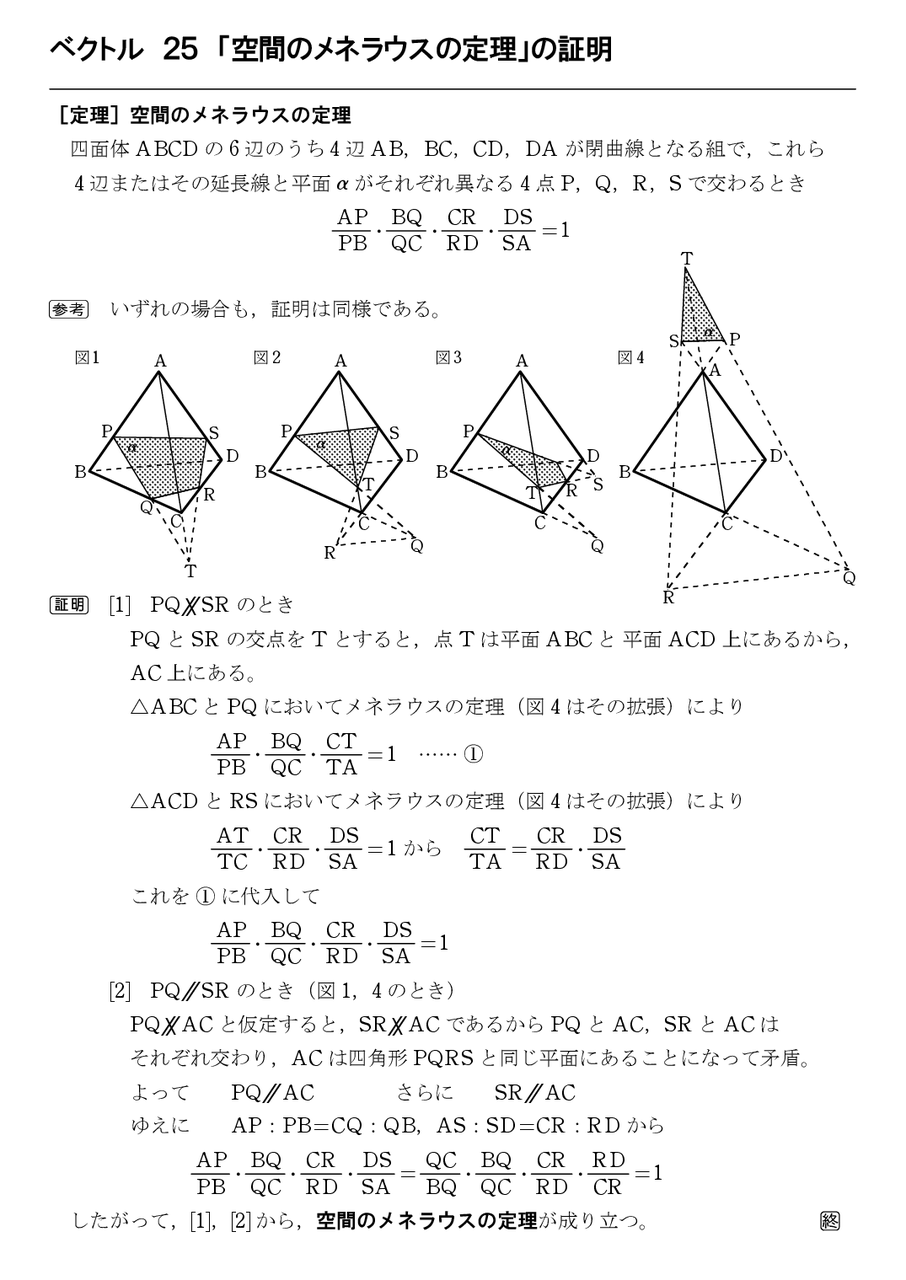



ベクトル 25 空間のメネラウスの定理 の証明 怜悧玲瓏 高校数学を天空から俯瞰する




チェバの定理の証明 覚え方を早稲田生が紹介 問題付き 高校生向け受験応援メディア 受験のミカタ




チェバメネラウスとかは解けるのですが底辺が同じなら高さが同じと言われても高さ が Clear




チェバ メネラウスの定理が分かるようになる 個人指導シグマ 中高一貫 国立生専門塾




Ppt 数学のかた ち Powerpoint Presentation Free Download Id




平面幾何 3 メネラウスの定理の拡張と逆 怜悧玲瓏 高校数学を天空から俯瞰する




チェバの定理 メネラウスの定理が分からないのは 個人指導シグマ 中高一貫 国立生専門塾




改訂版 3trial数学a P121 3 チェバの定理 メネラウスの定理




連続投稿になってしまい申し訳ないのですが この問題の 2 が分かりません Clear




改訂版 4step数学a P129 3 チェバの定理 メネラウスの定理



メネラウスの定理とは 証明や覚え方 問題の解き方 受験辞典



3分で分かる チェバの定理をわかりやすく 証明も徹底解説 合格サプリ




2 164 Abc P Zbpc Zcpa Apb See How To Solve It At Qanda



3分で分かる チェバの定理をわかりやすく 証明も徹底解説 合格サプリ




チェバの定理 メネラウスの定理を使う問題再び 2017年度前期日程の奈良女子大学環境学部入試問題 身勝手な主張
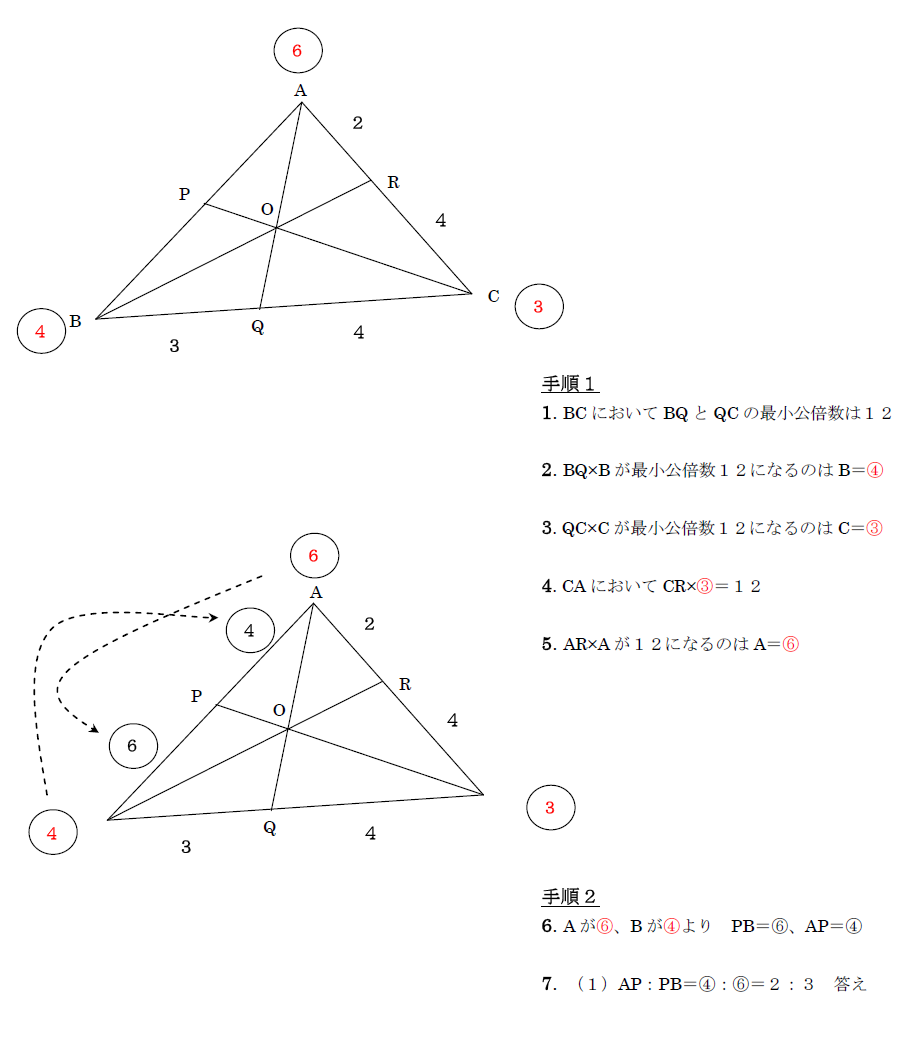



受験 定期試験 数学解き方集 裏技 解法 メネラウス チェバの定理 中学 高校




高校数学a チェバの定理1 基本 練習編 映像授業のtry It トライイット




2 164 Abc P Zbpc Zcpa Apb See How To Solve It At Qanda
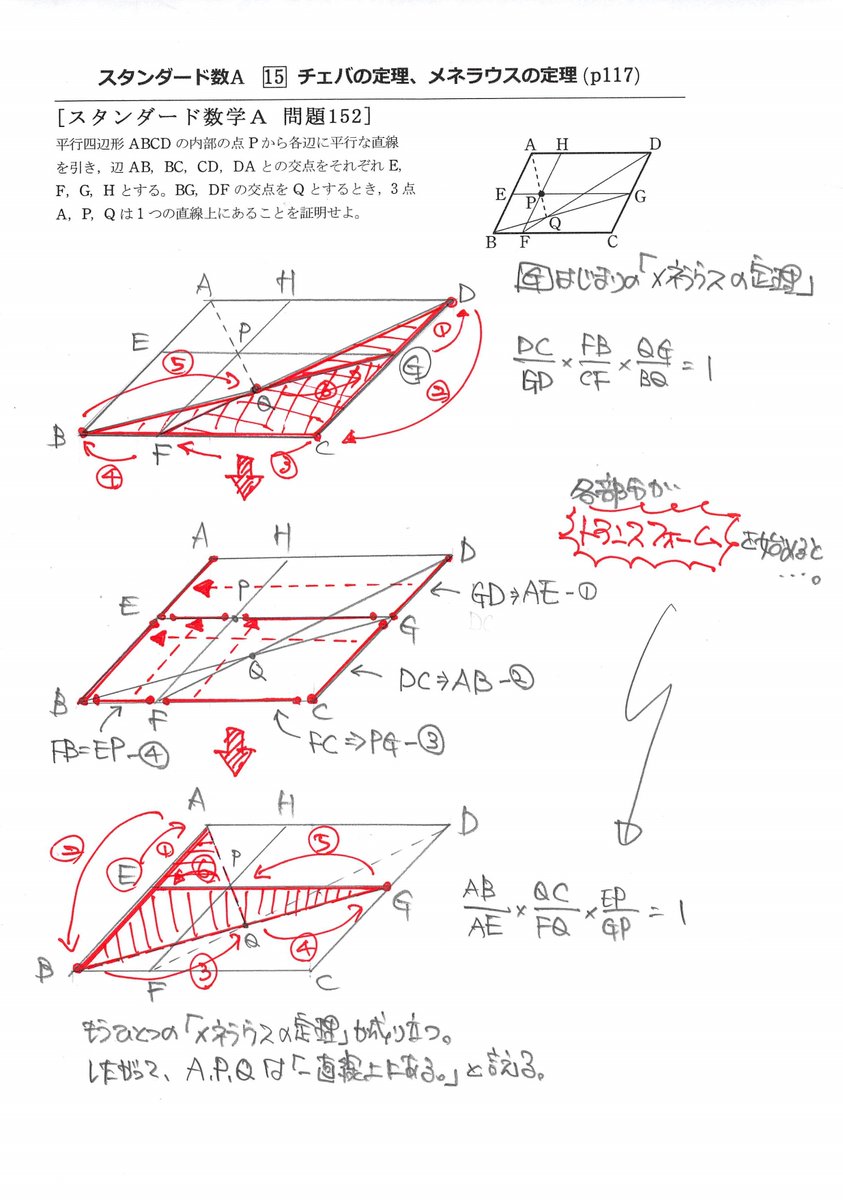



Twitter पर S Live数学館 数研スタンダード数a 2章 図形の性質 15チェバの定理 メネラウスの定理 問題152 P117 出題者は きっとsf好きに違いないですね 何しろ 平行四辺形が トランスフォーム して 新たな平行四辺形ができるのですから Sf




裏技公開 チェバもメネラウスも不要の解き方 必要なのは 最小公倍数と足し算だけ Youtube




2直線の交点 の裏技解法を知ろう 3パターンの解法




まだ公式まる覚えして消耗してるの チェバ メネラウスの定理 Youtube




改訂版 クリアー数学a P132 12 チェバの定理 メネラウスの定理



チェバの定理とは 証明や覚え方 メネラウスの定理との違い 受験辞典




箱ひげ図 チェバの定理とメネラウスの定理 あなたは解けますか 1冊でしっかりわかる と大人気のベストセラーシリーズに 待望の高校数学が登場 かんき出版のプレスリリース




高校 数学a 図形20 メネラウス定理2 10分 Youtube




チェバ メネラウスの定理の練習問題 9 Youtube




チェバの定理の証明 覚え方を早稲田生が紹介 問題付き 高校生向け受験応援メディア 受験のミカタ




平面ベクトル 2直線の交点 メネラウス型 オンライン無料塾 ターンナップ Youtube




メネラウスの定理



メネラウス




チェバの定理の証明 覚え方を早稲田生が紹介 問題付き 高校生向け受験応援メディア 受験のミカタ




即効 10点 大学入試 数学a ちょっとズルして 三角形の比の問題で 10点up For Android Apk Download




平面図形18 メネラウスの定理の逆 怜悧玲瓏 高校数学を天空から俯瞰する




チェバの定理の証明 覚え方を早稲田生が紹介 問題付き 高校生向け受験応援メディア 受験のミカタ




線分比問題 空間のメネラウスの定理 ベクトル Youtube




高校数学b 2直線の交点の位置ベクトル ベクトル分野ダントツno 1頻出問題 受験の月




授業での雑談ネタ 怜悧玲瓏 高校数学を天空から俯瞰する




平面幾何 2 チェバの定理の拡張と逆 怜悧玲瓏 高校数学を天空から俯瞰する



メネラウス の 定理 ビデオ ニュース




慶應生紹介 メネラウスの定理の覚え方はコレだ 証明 問題付き 高校生向け受験応援メディア 受験のミカタ




高校数学a メネラウスの定理とその逆の証明 受験の月




慶應生紹介 メネラウスの定理の覚え方はコレだ 証明 問題付き 高校生向け受験応援メディア 受験のミカタ




慶應生紹介 メネラウスの定理の覚え方はコレだ 証明 問題付き 高校生向け受験応援メディア 受験のミカタ



数学教えてください Sugaku048te Twitter
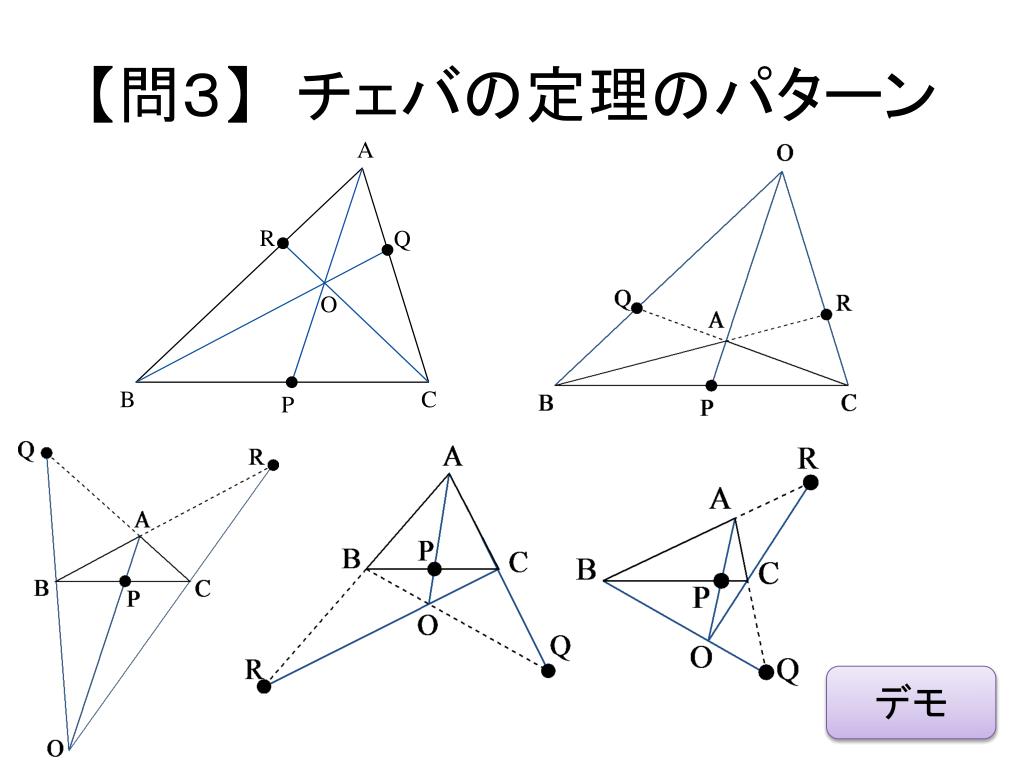



Ppt 数学のかた ち Powerpoint Presentation Free Download Id




箱ひげ図 チェバの定理とメネラウスの定理 あなたは解けますか 1冊でしっかりわかる と大人気のベストセラーシリーズに 待望の高校数学が登場 かんき出版
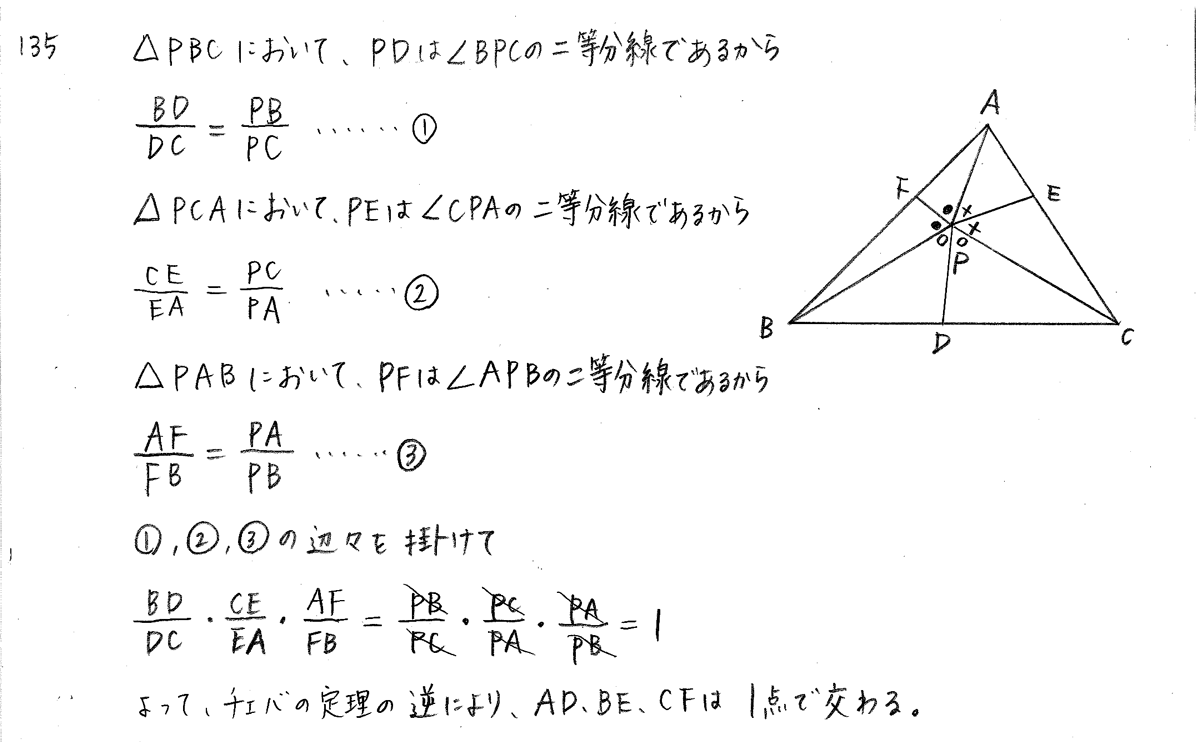



クリアー数学a 数a P121 補 チェバの定理の逆 メネラウスの定理の逆



チェバの定理 数学入試問題



チェバの定理とは 証明や覚え方 メネラウスの定理との違い 受験辞典



チェバの定理とは 証明や覚え方 メネラウスの定理との違い 受験辞典



0 件のコメント:
コメントを投稿